# 引言
题目链接:https://leetcode.com/problems/container-with-most-water/description/
# 题目大意
给定 n 个非负整数 a1,a2,...,an, 其中每个代表一个点坐标 (i,ai), 通过每个点做 x 轴的垂直线,最后取任意两条线,使得两条线与 x 轴所构成的容器能装最多的水。
Note: You may not slant the container and n is at least 2.(即水的面积不是容器的面积,而是最大矩形的面积,并且一定有解)
- Example
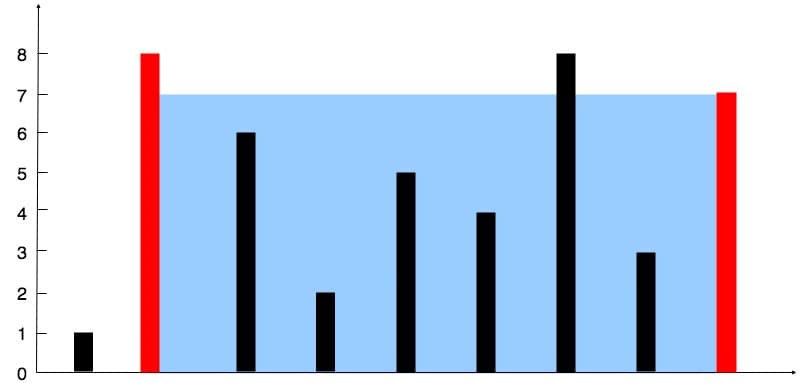
Input: [1,8,6,2,5,4,8,3,7]
Output: 49
# 题解
解题思路:
按照常识 (木桶原理), 两条线段构成的容器有效高度由较短的一边确定,整个容器的面积由坐标点 index 的差值和有效高度共同确定.
采取如下方式,首先确定一个条件的最优值,通过不断调优另一个条件值同时联动调整当前条件的值并跟踪最大值即可
即开始选择最大 index 差值,即数字序列第一个和最后一个 (这里用 l,r 表示);然后考察容器有效高度。若 height[l] > height[r] , 那么舍弃 r, 取 r 前一个考察,否则取 l 后一个考察,整个过程计算容器有效容积 area=min(height[right],height[left])∗(right−left) , 并不断维护即可
# 复杂度
时间复杂度 O(n)
空间复杂度 O(1)
# AC 代码
c++ 版本
class Solution | |
{ | |
public: | |
int maxArea(vector<int> &height) | |
{ | |
int l = 0; | |
int r = height.size() - 1; | |
int maxn = 0; | |
while (l < r) | |
{ | |
maxn = max(maxn, min(height[l], height[r]) * (r - l)); | |
if (height[l] < height[r]) | |
{ | |
++l; | |
} | |
else | |
{ | |
--r; | |
} | |
} | |
return maxn; | |
} | |
}; |
go 版本
func max(a, b int) int { | |
if a > b { | |
return a | |
} | |
return b | |
} | |
func min(a, b int) int { | |
if a < b { | |
return a | |
} | |
return b | |
} | |
func maxArea(height []int) int { | |
l, r := 0, len(height)-1 | |
var maxn int | |
for l < r { | |
maxn = max(maxn, min(height[l], height[r])*(r-l)) | |
if height[l] < height[r] { | |
l++ | |
} else { | |
r-- | |
} | |
} | |
return maxn | |
} |