# 引言
题目链接:https://leetcode.com/problems/generate-parentheses/description/
# 题目大意
给出数字 n, 生成共有 n 对括号的所有正确的形式,有效形式见例子
- Example
For example, given n = 3, a solution set is:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
# 题解
# 一句话题解
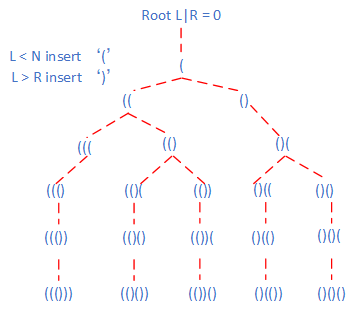
如下图所示此题结果是一颗二叉树根节点到每个叶子节点的路线集合 (已经略去不符合题目要求的无效结果), 利用递归 + 回溯的搜索过程即可完成这个过程,要结果有效需要满足如下条件,利用条件合理剪枝,dfs 搜索即可
// 合理化剪枝
if (l < n) insert('(')
if (r < l) insert(')')
# 复杂度
时间复杂度 O(2^n)
空间复杂度 O(n)
# AC 代码
c++ 版本
class Solution | |
{ | |
public: | |
vector<string> generateParenthesis(int n) | |
{ | |
vector<string> ret; | |
dfs(1, 0, n, "(", ret); | |
return ret; | |
} | |
private: | |
void dfs(int l, int r, const int n, string cur, vector<string> &ret) | |
{ | |
if (n == l && n == r) | |
{ | |
ret.push_back(cur); | |
return; | |
} | |
if (l < n) | |
{ | |
cur.push_back('('); | |
dfs(l + 1, r, n, cur, ret); | |
cur.pop_back(); | |
} | |
if (r < l) | |
{ | |
cur.push_back(')'); | |
dfs(l, r + 1, n, cur, ret); | |
cur.pop_back(); | |
} | |
} | |
}; |
go 版本
func dfs(l, r, n int, cur string, ret *[]string) { | |
if n == l && n == r { | |
*ret = append(*ret, cur) | |
return | |
} | |
if l < n { | |
cur += "(" | |
dfs(l+1, r, n, cur, ret) | |
cur = cur[0 : len(cur)-1] | |
} | |
if r < l { | |
cur += ")" | |
dfs(l, r+1, n, cur, ret) | |
cur = cur[0 : len(cur)-1] | |
} | |
} | |
func generateParenthesis(n int) []string { | |
var ret []string | |
dfs(1, 0, n, "(", &ret) | |
return ret | |
} |